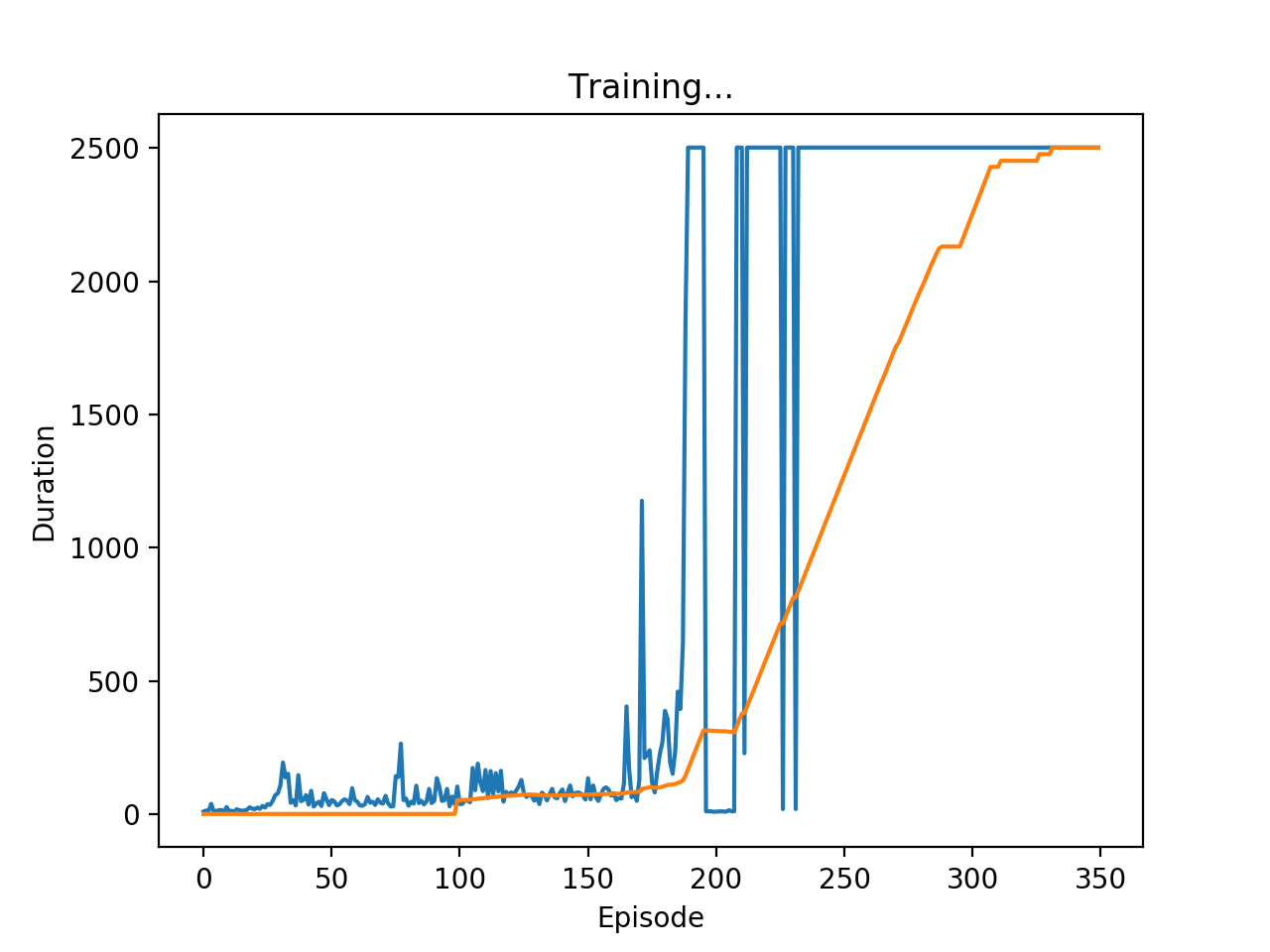
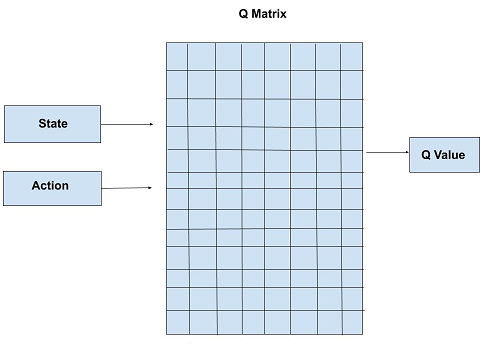
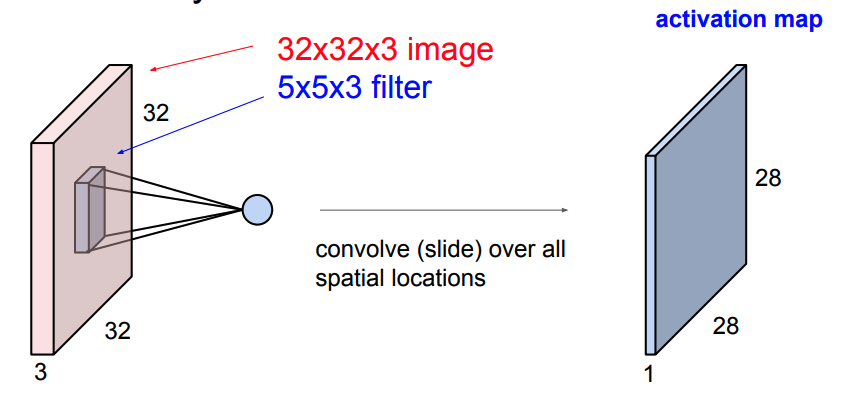
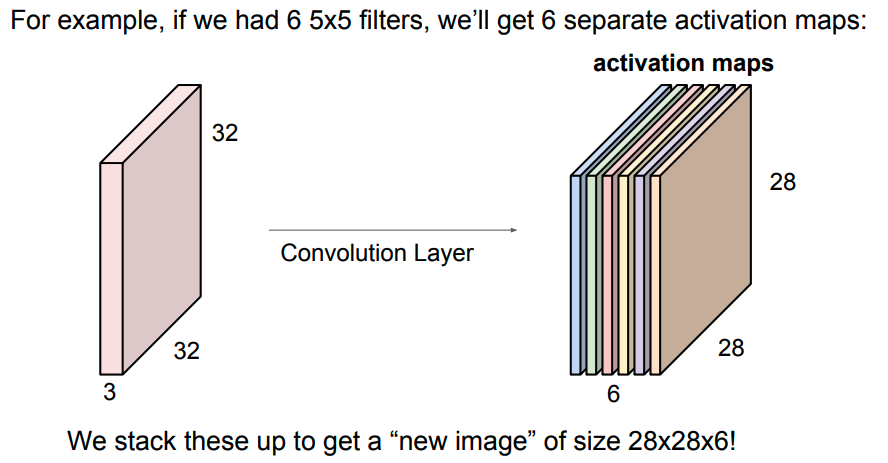
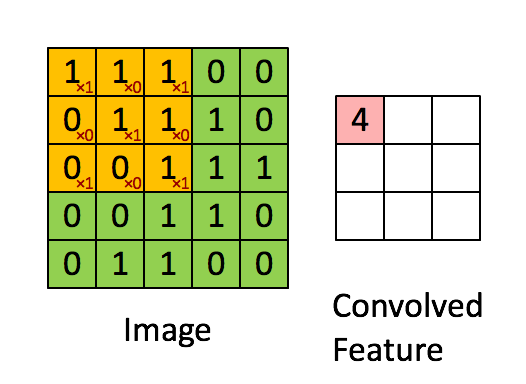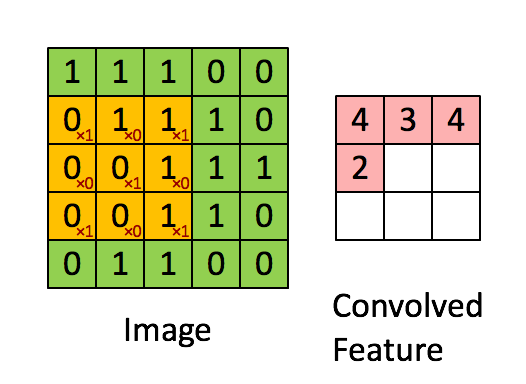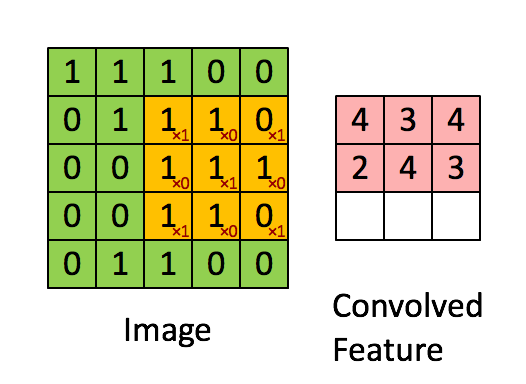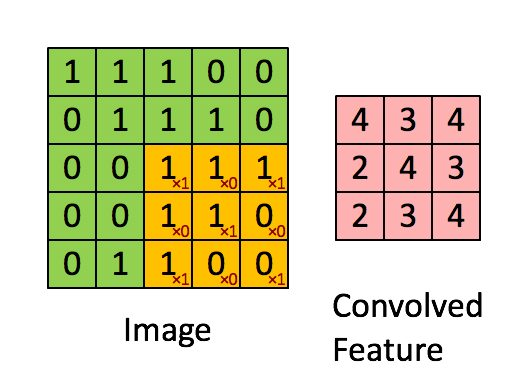
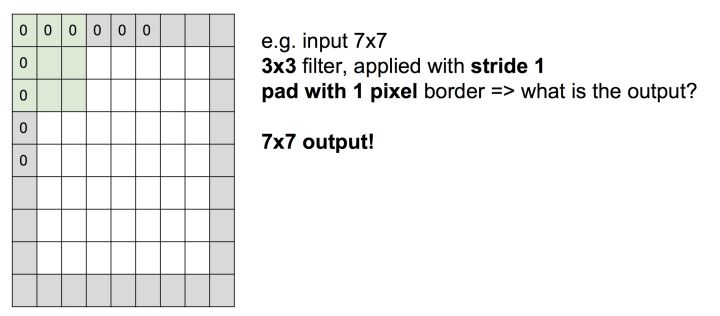
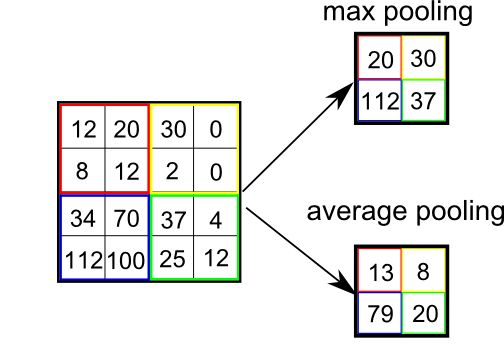
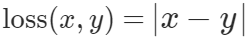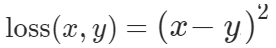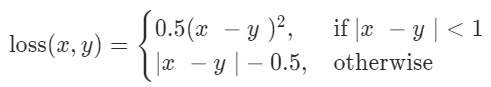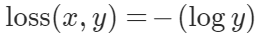看到标题,有的人可能会奇怪,为什么要把道家思想和达尔文主义并列。我这里简单引用几句话大家就明白了:“圣人处无为之事,行不言之教”,“天地不仁,以万物为刍狗;圣人不仁,以百姓为刍狗”,“道常无为而无不为,侯王若能守之,万物将自化”,“其政闷闷,其民淳淳;其政察察,其民缺缺”,“圣人之道,为而不争”,这些都是道德经里面的话,道家是崇尚无为的,认为万物可以自化。再看看达尔文的进化论:“物竞天择,适者生存”,是不是同一个道理,我们都知道进化论不是基督教的信仰,而当时的欧洲的有识之士普遍对中国文化有所研究,达尔文的思想是不是受道家启发呢?暂时不得而知,但是逻辑是一样的。除了达尔文,还有重农学派提倡的放任自由的经济制度,亚当斯密的自由市场理论,都是和道家思想类似的。还有一句话中国人比较熟悉“不管白猫和黑猫,能抓到老鼠就是好猫”,这句话是为了证明市场经济合理性的。显然,以上思想都是可以归为一类的。
四十年前,有人提出要全面的理解伟人的思想,并在伟人著作的选集中增加一篇《反对本本主义》,并强调“实践是检验真理的唯一标准”,当然“实践论”也依然是伟人的名篇,但说法却不是这个说法,《实践论》强调的是“理论要结合实际,经验是理论的前提”是有很深的哲学方法论的,但是“实践是检验真理的唯一标准”这句话则有着强烈的成王败寇色彩。但必须承认这些话都是非常雄辩的,观点是非常有力的。于是受此启发,也就写了这篇“完整的理解道家思想和达尔文主义”。我认为,道家思想和达尔文主义是右派的最根本的理论基础,这是他们雄辩的部分,而他们错误的部分则是未能完整的理解道家思想和达尔文主义。
儒生和道家的争论。。。。汉景帝也是很没出息,他应该说如果朕做出违背人民的事情,也会受到一样的下场。这个道生的意思,就是君王再坏也是君王,臣下也不能弑君。这个感觉就像,有钱就是厉害,贪污也是人家的本事,口气是不是很像?就很明显没有真正理解道德经,汤武革命正是天地不仁以万物为刍狗的合理性结果。而圣人不仁所以百姓为刍狗的百姓,显然是包含贵族在内的,那时如果说下等人那叫做黎民,不叫百姓,有姓的都是贵族。所谓以百姓为刍狗,就是不管你是王公贵族还是黎民百姓,在圣人眼中都是刍狗,都是平等的。我这么解释也许有人会认为我是附会老子的意思,那么我们看看庄子的思想是什么。庄子是道家仅次于老子的重要人物。庄子在齐物论充分表达了什么叫做以万物为刍狗,那就是万物都是平等的,没有高低贵贱之别,这样怎么会存在一个不可以被推翻的君主呢?
社会达尔文主义的普遍错误。
进化论的翻译有问题,应该翻译为演化论。
演化论的意思是,把你丢到大草原上,你要么成为狮子,要么成为鬣狗,或者成为斑马,把你丢到猪圈里面,你必须变成一只猪才是适应环境的。把你丢到猪圈里面,你还想做人可以吗?按照演化论的规律来说,你在猪圈里面做人,就会饿死。演化论没有错,但把在猪圈里面做猪当作理想社会,那就是你的错了。
庄子在达生篇有一个小寓言,祭祀官穿着黑色礼服,一本正经地来到猪圈,劝说猪:“你干嘛厌恶死亡呢?我要饲养你三个月,然后戒十天,斋三天,用白茅作垫席,准备一张雕绘精美的案几,把你摆在上面去祭祀神灵,那么你愿意做吗?”替猪着想的话,一定会说,这样还不如拿糟糠喂养它,把它关在猪圈里呢;为人自身考虑的话,假如活着能享有高官厚禄的尊贵,死了能用华丽的装载灵柩的车子拉着,下葬时享受豪华的棺椁,那么就会去做。替猪着想的话,那就抛弃白茅彫俎;为自己打算就拼命追求轩冕腞楯聚偻。人与猪的不同之处是什么呢?庄子的意思很明显,追求自由,不是让你们在那里自我摧残的,连猪都知道不该追求那些虚头巴脑的东西,人干嘛要整那些没用的呢?
道家思想从来都是讲为而不争,而不是自由竞争。什么叫为而不争,我觉得和孔子说的君子和而不同,是一个意思。孔子说,君子和而不同,小人同而不和。小人都是一个样的,整体就知道争。君子呢,努力做事,但是从来不争。
丛林法则的有效的基础是绝对公平的游戏规则。基因的进化是不可以父传子的,更是不可以窃取公器的。达尔文主义是个体的竞争,田径比赛,高考,并且要禁止开小灶,才能达到优选优育的目的。公平是进化论的基础。关于生育部分也就不多说了,达尔文主义也要求一部分人应该多生育。基督教的一夫一妻制根本就不符合进化论的思想。在一夫一妻制下谈社会达尔文主义是没有意义的,因为你再怎么竞争也没有扩大你的遗传优势,没有遗传优势也就没有所谓演化。
优胜劣汰是市场经济的常用话语,但究竟是优胜劣汰还是劣币驱逐良币,我觉得要一分为二的看。大量的事实已经证明在没有强力监管的情况下是劣币驱逐良币而不是优胜劣汰。比如说,环境污染,那肯定是不治理污染的成本低,驱逐主动治理污染的,抄袭盗版的成本低驱逐自主研发的,无视劳工人权的成本低驱逐福利优厚的,官商勾结的成本低驱逐合法经营的。
人与动物最大的区别之一就是人可以制定规则,也可以改变规则,但动物无法改变人类给他们制定的规则。既然人有了动物所不具有的制定规则的能力,那么人类就应该制定一个属于人类的规则,而不是给人类制定一个动物的规则。
老子强调,为而不有,功成而弗居,老子是反对私有财产的,老子也是反对物质享受的。那么消费主义就不符合道家思想。
完整的理解猫论。不管白猫黑猫抓到老鼠就是好猫。这里的猫和老鼠究竟指什么?白猫黑猫是计划与市场,老鼠就是目标,这个目标是什么?这个目标是社会主义。让一部分人先富起来,这个目标就是最终实现共同富裕。如果你认为老鼠是一部分人先富起来,那么就大错特错了。
为什么闲的没事写这些玩意儿呢?因为市场竞争挺无聊的,以我们这些智商和那些蝇营狗苟的人竞争,一群野狗争抢食物,对外杀敌的时候,没多少输出,抢起食物来却非常起劲,我们的力量是用来对外的,不是用来对内的。还是老子那句话,为而不争。搞内部倾轧的竞争,厚黑学,对有修养的人来说,是很丢脸的一件事。
孔孟为什么伟大,因为孔孟肯定了革命的合法性。为什么要批孔呢?因为儒家已经被后生所篡改,将忠君变成了儒家教条的一部分,其实儒家一直认为民为贵、社稷次之、君为轻,而且肯定汤武革命,既然肯定汤武革命就不可能把忠君作为教条,即便董仲舒的天人感应,五德终始,也是劝喻君王,不好好干就要下台。但是后来儒家被偷换概念,成为了精英的代名词,这个转换与科举制有一定关系。也就是通过垄断知识来垄断权力,皇权与知识分子结成了牢固的联盟,这个在宋朝发展到了顶点。所以文革批孔,批的其实是精英意识,而不是批的革命意识。
汤武当然可以革命!
今天的新儒学复兴,一定要注意甄别,复兴的是精英意识还是革命意识,如果是精英意识,那么就要毫不留情的打倒他,如果是革命意识,那么说明就领悟到了儒家的精髓,就可以拥护他。
明朝时,儒生们积极的评议朝政,只可惜明朝仍然有很多制度上的缺陷,还是覆亡了。明朝覆亡后,孔孟的精神没有消失,西移到了法国。