强化学习简介（三）：DQN

上一个例子中我们使用了冰面滑行的游戏环境，这是一个有限状态空间的环境。如果我们现在面对的是一个接近无限的状态空间呢？比如围棋，比如非离散型的问题。我们无法使用一个有限的Q表来存储所有Q值，即使有足够的存储空间，也没有足够的计算资源来遍历所有的状态空间。对于这一类问题，深度学习就有了施展的空间了。

Q表存储着状态s和动作a、奖励r的信息。我们知道深度神经网络，也具有存储信息的能力。DQN算法就是将Q-table存储结构替换为神经网络来存储信息。我们定义神经网络`f(s, w) ~~ Q(s)`，输出为一个向量`[Q(s, a_1), Q(s, a_2), Q(s, a_3), …, Q(s, a_n)]`。经过这样的改造，我们就可以用Q-learing的算法思路来解决更复杂的状态空间的问题了。我们可以通过下面两张图来对比Q-learning和DQN的异同。

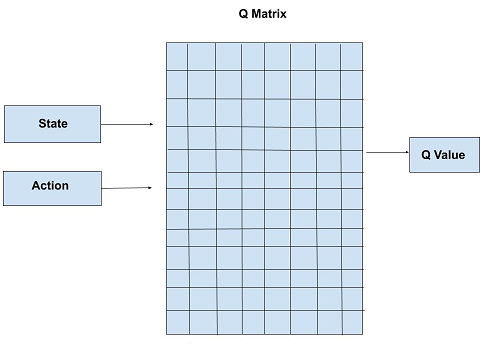
Q-learning

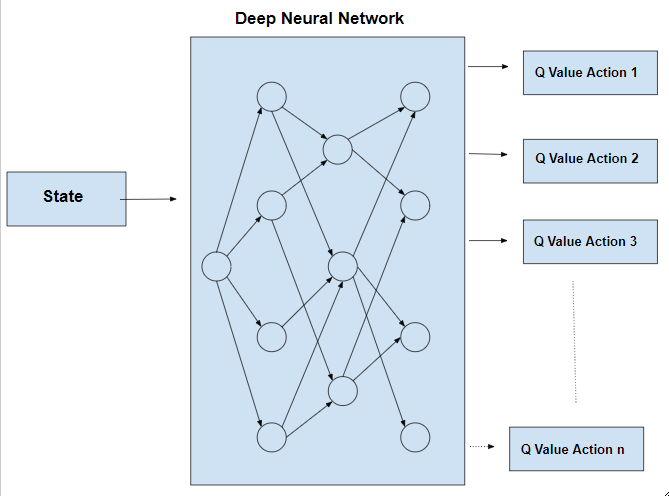
Deep-Q-learning

网络结构要根据具体问题来设计。在神经网络训练的过程中，损失函数是关键。我们采用MSE来计算error。

`L(w) = (ubrace(r + argmax_aQ(s’, a’))_(目标值) - ubrace(Q(s, a))_(预测值))^2`

基本算法描述

使用随机参数初始化网络Q
while 未收敛:
  action 按一定概率随机选取，其余使用argmax Q(s)选取
  模拟执行 action 获取 状态 s_, 奖励 r, 是否完成 done
  if done:
    target = r
  else:
    target = r + gamma * argmax Q(s_)
  loss = MSE(target, Q(s, a))
  使用loss更新网络Q
  s = s_

但是，通过实验我们会发现，训练过程非常的不稳定。稳定性是强化学习所面临的主要问题之一，为了达到稳定的训练我们需要运用一些优化的手段。

环境的稳定性

Agent生活在环境之中，并根据环境的反馈进行学习，但环境是否是稳定的呢？假设agent在学习出门穿衣的技能，它需要学会在冬天多穿，夏天少穿。但是这个agent只会根据当天的反馈来修正自己的行为，也就是说这个agent是没有记忆的。那么这个agent就会在多次失败后终于在冬天学会了多穿衣，但转眼之间到了夏天他又会陷入不断的失败，最终他在夏天学会了少穿衣之后，又会在冬天陷入失败，如此循环不断，永远不会收敛。如果要能够很好的训练，这个agent至少要有一整年的记忆空间，每一批都要从过去的记忆中抽取记忆来进行训练，就可以避免遗忘过去的教训。

在DeepMind的Atari 论文中提到

First, we used a biologically inspired mechanism termed experience replay that randomizes over the data, thereby removing correlations in the observation sequence and smoothing over changes in the data distribution.

意思是，受生物学启发，他们采用了一种叫做经验回放（experience replay）的机制，随机抽取数据来到达“移除观察序列的相关性，平滑数据分布的改变”的目的。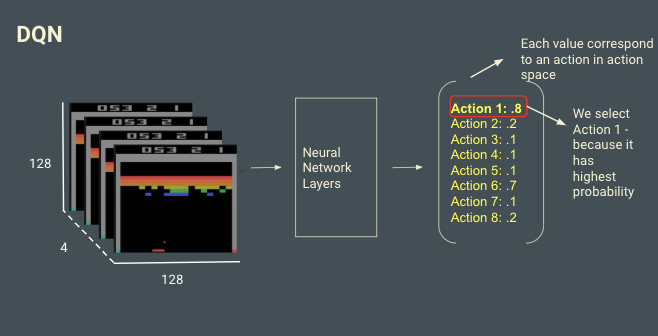
DQN with Atari

我们已经理解了要有经验回放的记忆，但是为什么一定要随机抽取呢？对此论文认为这个随机抽取可以移除序列相关性、平滑分布中的改变。当如何理解呢？简单的说就是在我们不清楚合理的周期的情况下，能够保证采样的合理性。我们仍然以四季穿衣举例，假设我们不使用随机采样，我们必须在每次训练中都采用365天左右的数据，才能使我们的数据样本分布合理。可是agent并不清楚一年365天这个规律，这恰恰是我们所要学习的内容。采用随机采用，就可以自然的做到数据的分布合理，而且只需要使用记忆中的部分数据，减少单次迭代的计算量。

在这个记忆里，我们并不记录当时的网络参数（分析过程），我们只记录（状态s，动作a，新状态s’, 单步奖励r)。显然，记忆的尺寸不可能无限大。当记忆体增大到一定程度之后，我们采用滚动的方式用最新的记忆替换掉最老的记忆。就像在学习围棋的过程中，有初学者阶段的对局记忆，也有高手阶段的对局记忆，在提升棋艺的角度来看，高手阶段的记忆显然比初学者阶段的记忆更有价值。

说句题外话，其实对于一个民族而言也是一样的。我们这个民族拥有一个非常好的传统，就是记述历史，也就是等于我们这个民族拥有足够大的记忆量，这是我们胜于其他民族的。但是这个历史记录中，掺杂了历史上不同阶段的评价，这些评价是根据当时的经验得出的。而根据DQN的算法描述来看，对我们最有价值的部分其实是原始信息，而不是那些附加在之上的评价，这些评价有正确的部分，也有错误的部分，我们不用去过多关心。我们只需要在今天的认知（也就是最新的训练结果）基础上，对历史原始信息（旧状态、动作、新状态、单步奖励）进行随机的抽样分析即可。

网络稳定性

DQN另一个稳定性问题与目标值计算有关。因为`target = r + gamma * argmax Q(s’)`，所以目标值与网络参数本身是相关，而参数在训练中是不断变化的，所以这会造成训练中的不稳定。一个神经网络可以自动收敛，取决于存在一个稳定的目标，如果目标本身在不断的游移变动，那么想要达到稳定就比较困难。这就像站在平地上的人很容易平衡，但如果让人站在一个不断晃动的木板上，就很难达到平衡。为了解决这个问题，我们需要构建一个稳定的目标函数。

解决的方法是采用两个网络代替一个网络。一个网络用于训练调整参数，称之为策略网络，另一个专门用于计算目标，称之为目标网络。目标网络与策略网络拥有完全一样的网络结构，在训练的过程中目标网络的参数是固定的。执行一小批训练之后，将策略网络最新的参数复制到目标网络中。

目标网络

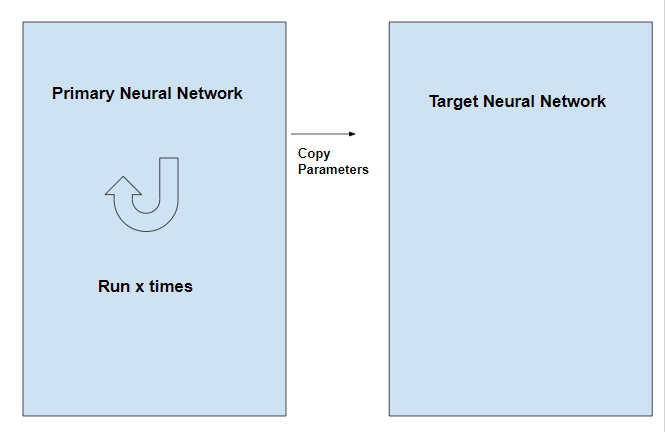
经验回放和目标网络的效果见下表（引用自Nature 论文）：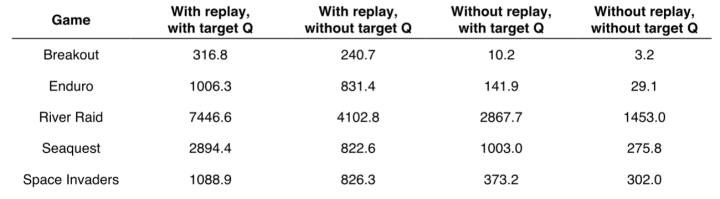
优化对比

其他DQN优化

关于DQN的优化，这篇文章描述的比较全面 https://zhuanlan.zhihu.com/p/21547911。在之后的实践中考虑是否进一步深入。主要介绍3个改进：

DQN优化

Double DQN：对目标值计算的优化，a’使用策略网络选择的动作来代替目标网络选择的动作。
Prioritised replay：使用优先队列（priority queue）来存储经验，避免丢弃早期的重要经验。使用error作为优先级，仿生学技巧，类似于生物对可怕往事的记忆。
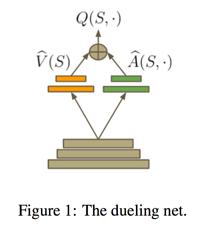
Dueling Network：将Q网络分成两个通道，一个输出V，一个输出A，最后再合起来得到Q。如下图所示（引用自Dueling Network论文）。这个方法主要是idea很简单但是很难想到，然后效果一级棒，因此也成为了ICML的best paper。

Dueling Network

2019-12-28